Frequency domain channel linear equalizationbasics

Let represent the input signal, represent the channel response, represent the receiver side noisen. N_t and N_r is the number of transmitting and receiving antennas, respectively. The received signal is: .

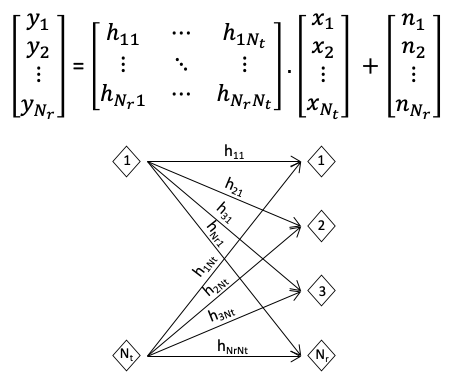
Let's define the following:

• Auto-correlation of x:
• Auto-correlation of n:
• Cross-correlation of x and n:
• Cross-correlation of n and x:

Linear equalization means to apply a matrix to y, in order to get an estimation of x, denoted as :, where different W corresponds to different types of equalizers.

Zero Forcing (ZF) equalizer

A ZF Equalizer fully inverses the impact of the wireless channel. It applies the (pseudo) inverse of the channel frequency response to the received signal. I.e., , and

Note cannot be inverted if its rank is less than N_t. This may happen when e.g. , or when the channel is highly correlated. In such case, ZF equalization of the received signal cannot be performed and the original signal cannot be recovered.

Minimum Mean Square Error (MMSE) equalizer

A MMSE equalizer tries to minimize the MSE of the residual error : 

e is minimized when e and y is orthogonal (otherwise, we can always use the information of y to reduce e). I.e.,

Now let's expand the above formula:

Note Being able to derive the equalization matrix W does not mean the transmitted signal can be re-constructed. In order to do so, it must also satisfy . E.g. if , the signals sent from the two transmitter antennas must be generated from the same stream of input source. One popular example of such case is the Alamouti code.

Equalization in a Single Input Single Output (SISO) system

In a SISO system, the aforementioned equations can be simplified:

• Zero Forcing:
  • where '*' denotes conjugation.
• Minimum Mean Square Error:

In the example below, it is assumed:

• noise follows Gaussian distribution with
• the transmitted signals across different transmit antennas are not correlated, and the transmit power is P at each antenna, i.e.
• With assumptions above, the MMSE equalizer is simplified to: , where represents the Signal to Noise Ratio (SNR).